Lösa Kakuro-pussel

I den här guiden erbjuder vi en rad praktiska tips om hur man löser Kakuro-pussel, med svårigheter som sträcker sig från nybörjare till expertnivå.

För att sammanfatta reglerna: Kakuro är ett pusselspel på ett korsordliknande bräde där siffror används för att få dem att sammanfatta de värden som anges i brädans definitionsrutor. Dessutom, inom varje summgrupp, varje siffra kan visas högst en gång.

Det traditionella sättet att lösa ett Kakuro-pussel är inkrementellt: genom att använda befintlig information på tavlan kan du med säkerhet hitta värdet på en specifik cell som bara kan ta ett möjligt värde. Sedan fylls det värdet och processen upprepas tills alla kortceller har upptäckts.

I vissa situationer, det finns ingen specifik kortcell som bara har en möjlighet. I dessa fall måste var och en av möjligheterna undersökas på egen hand och elimineras genom motsägelser tills endast en åtgärd återstår.

Presenterades nedan flera metoder för att göra framsteg när det gäller att lösa själva pusslet.

Unika summor för specifika definitioner

Det finns några definitioner som endast kan lösas på ett specifikt sätt:

• summan 3 (över två celler) kommer alltid att vara 1 + 2.
• summan 4 (över två celler) kommer alltid att vara 1 + 3.
• summan 17 (över två celler) kommer alltid att vara 8 + 9.
• summan 6 (över tre celler) kommer alltid att vara 1 + 2 + 3.
• summan 24 (över tre celler) kommer alltid att vara 7 + 8 + 9.

och så vidare... Vanligtvis kan du sväva över ett Kakuro-rutnät över definitionsnumret och ett verktygstips visas som innehåller alla möjligheter att skriva summan med unika siffror i antalet tillgängliga celler.

De belopp som kan skrivas på ett unikt sätt är vanligtvis låga summor eller höga summor som tvingar låg/höga siffror i svaret för att uppnå dem.

Att ha ett unikt sätt att skriva summan hjälper, men kom ihåg att alla permutationer är giltiga och du måste fortfarande ta reda på vilken faktisk permutation som ska användas på tavlan.

Rad- eller kolumnbegränsningar

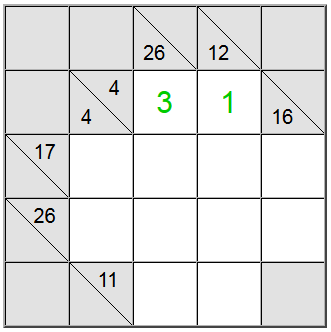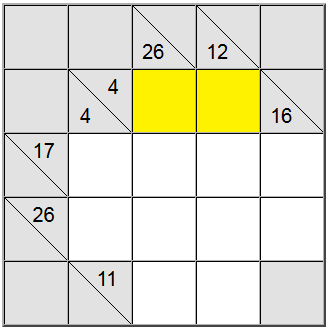
För de gula cellerna markerade ovan finns det bara ett sätt att skriva summan: 4 = 1 + 3. Men vi måste fortfarande ta reda på vilken permutation (1 + 3 eller 3 + 1) som ska användas.

Visar sig att den 26 vertikala definitionen hjälper oss: en summa över 4 celler som skulle innehålla siffran 1 skulle vara högst 1 + 9 + 8 + 7 = 25. Eftersom vår summa är 26 visar det sig att siffran 1 inte kan vara en del av summan. Därför är den enda återstående ordningen för de gula rutorna 3 + 1.

Definitioner korsningar

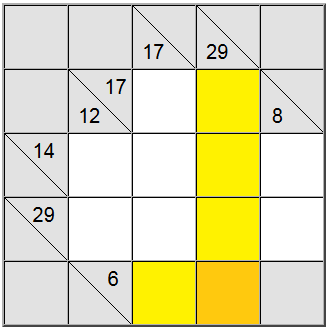
På brädet ovan kan de horisontella gula rutorna skrivas som 6 = 1 + 5 eller 6 = 2 + 4. Den vertikala gula summan kan endast skrivas som 29 = 5 + 7 + 8 + 9.

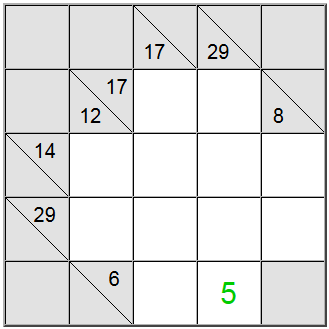
Den gula fyrkanten som finns i skärningspunkten mellan dessa två summerdefinitioner måste innehålla samma siffra, så det måste finnas en gemensam siffra i de horisontella och vertikala definitionerna för att kunna delas mellan dem. Genom att titta på möjligheterna ovan kan vi lätt räkna ut det 5 är den enda siffran som respekterar detta kriterium.

Denna teknik fungerar särskilt bra när man skär en lågsumma med en högsummadefinition. Definitioner med låg summa och hög summa är de som har ett relativt lågt eller högupplöst nummer (6 respektive 29 för vårt exempel) jämfört med antalet tillgängliga celler. Eftersom 6 är relativt låg kommer det att tvinga låga siffror i summerpresentationen, och 29 kommer att tvinga höga siffror (för att uppnå dessa summor med det givna antalet celler). Därför kommer skärningspunkten mellan låga och höga siffror sannolikt endast att innehålla en kandidat för det faktiska cellvärdet.

Min/ maxvärden för en sumgrupp

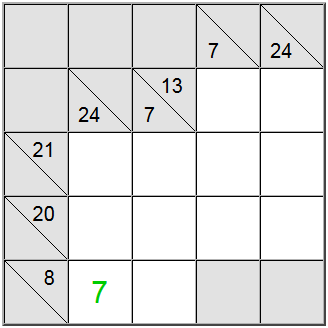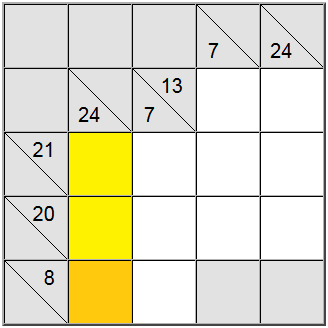
Ibland är det användbart att räkna ut max- eller minvärdet för en sumgrupp. Detta kan ge dig en känsla av vad som är det giltiga sifferintervallet för just den summan, vilket i sin tur hjälper dig att göra korrelation med andra begränsningar och räkna ut de unika uppdragen på tavlan.

I exemplet ovan accepterar de gula vertikala cellerna endast värden som är lika med 7 eller högre. Om du försöker tilldela en 6, kan du enkelt räkna ut att 6 + 9 + 8 = 23 så definitionssumman av 24 skulle inte vara uppnåelig.

Eftersom 7 är ett minimum, den horisontella definitionen med 8 som en summa tvingar 7 i den positionen.

Slutsats

Att öva är det bästa sättet att se hur detta råd kan tillämpas i faktiska Kakuro-spel. Spela ett pussel på riktigt. Vi önskar er lycka till och mycket roligt!

Spela Kakuro